为研究泄压条件下准静态压力峰值及其衰减规律,采用带有泄压口的长方形爆炸室开展了温压炸药内爆炸试验,获取了4种典型比例泄压面积下准静态压力时程曲线,分析了泄压口面积对准静态压力峰值及衰减规律的影响。结果 表明,随着泄压口面积的増加,准静态压力峰值、峰值到达时间、上升速率峰值和准静态持续时间均减小,而压力下降速率増加。泄压和密闭条件下的准静态压力峰值qA和q0与泄压口面积A和密闭空间容积V之间满足(qA)/(q0)=f(A/(V2/3))的函数关系,准静态压力q(t)满足q(t)/qA=f(A/V)的函数关系; 若峰值压力下降不大于10%时可忽略泄压对峰值的影响,则A/V2/3应不大于0.0085,与文献给出的A/V2/3≤0.0215相差较大; 在现有研究和试验数据基础上,建立了与试验结果吻合度较高的不同泄压口面积下实时准静态压力q(t)的经验公式,可用于泄压条件下的温压炸药内爆炸准静态压力预估。

To study the peak value of quasi-static pressure and its attenuation law under unsealed conditions, the internal explosion test of thermobaric explosive was carried out in a rectangular explosion vessel with a vent. The quasi-static pressure—time history curves under four typical venting areas were obtained, and the influence of venting area on the peak value of quasi-static pressure and its attenuation was analyzed. The results show that the peak quasi-static pressure, the peak arrival time, the duration of quasi-static pressure and the peak rising rate all decrease with increasing the venting area. On the contrary, the descent rate of pressure increases with increasing the venting area. If A, q(t), qA and q0 respectively represent the venting area, the volume of the explosion vessel, the quasi-static pressure at any time, the peak quasi-static pressure under unsealed conditions and that under sealed conditions, then the following functional relationships exist: qA/q0=f(A/V2/3), q(t)/ qA=f(A/V). If the decrease of the peak pressure is less than 10%, the influence of the explosion vent on the peak value can be neglected, and A/V2/3 should be not more than 0.0085, which is quite different from A/V2/3≤0.0215 given in literature. Based on the existing research and experimental data, the empirical formulas of q(t)under different venting areas are obtained, which are in good agreement with the experimental results. The empirical formulas can be applied to predict the quasi-static pressure of internal explosion of thermobaric explosives under unsealed conditions.

约束空间内爆炸是精确制导武器打击建筑、舰船等高价值目标的主要毁伤方式。准静态压力是内爆炸的主要压力毁伤元之一,侵彻孔洞、门窗、舱壁人孔等泄压结构对内爆炸准静态压力的形成和持续时间影响不可忽略。泄压口大小对内爆炸准静态压力的影响一直是研究的热点,特别是随着温压炸药在制导侵彻武器中的逐步应用,温压炸药在不同泄压条件下的内爆炸准静态压力特性研究具有重要的军事意义。

目前国内外相关的研究主要集中在密闭条件下的准静态压力峰值预测以及气体/粉尘等工业燃爆的泄压特性。Weibull^[1]研究了各种形状的排气口对封闭体内的准静态压力的影响,认为准静态压力只是装药质量m与容器容积V比值m/V的函数,当泄压口的面积A与封闭体的容积V满足A/ V^2/3≤0.0215时,可以忽略排气口的影响,这一结论也被大量研究人员采用。Proctor等^[2]、Kinney等^[3]发展了泄压结构中准静态压力时间历程理论。Baker^[4-5]等通过对化学爆炸和反应泄压分析,认为泄压条件下准静态压力峰值是A/V^2/3(比例泄压面积)的单值函数。赵天辉等^[6]开展了方形容器泄爆过程中的压力特性研究,认为小面积泄压导致容器内压力出现双峰,而大面积泄压对压力峰值影响较小。汪维等^[7]研究了建筑物内爆泄压口冲击波参数与不同结构参数之间的关系,给出了泄压口的冲击波参数计算经验公式。张玉磊、李鸿宾、王等旺、胡宏伟等^[8-12]研究了炸药在密闭条件下的准静态压力,给出了准静态压力峰值计算的经验公式。徐维铮等^[13-14]研究了装药质量和泄压口对约束空间内爆炸准静态超压载荷的影响规律,并给出了以封闭准静态超压峰值作为起始状态的泄压过程简化理论公式,但没有考虑泄压口对准静态压力峰值的影响。从国内外研究成果来看,有关泄压条件下准静态压力的理论研究集中在20世纪70和80年代,近期的研究主要集中在泄压条件下的冲击波特性或密闭条件下的准静态压力特性,有关泄压条件下准静态压力峰值及其衰减规律研究较少,温压炸药的相关研究几乎空白。

本实验通过带有泄压口大小可调的方形爆炸室研究泄压口面积对温压炸药内爆炸准静态压力的影响,获取了4种典型比例泄压面积条件下的准静态压力时程曲线,分析了泄压口面积对准静态压力峰值及衰减规律的影响,在现有研究成果和试验数据基础上,建立了与试验结果吻合度较高的不同泄压口面积下的准静态压力计算模型,以期为侵爆、半穿甲等内爆型温压战斗部准静态压力峰值及其衰减规律的预测提供支撑,并对温压弹药威力及毁伤预估提供参考。

试验装置为方形爆炸室,爆炸室外部长、宽、高分别为1.40、0.85和0.85m,壁厚10mm。爆炸室五面密封,在尺寸为0.85m×0.85m的一面中心开有直径500mm的孔,孔向外焊接法兰盘,用于安装中心开有不同大小泄压口的薄钢板。法兰盘自爆炸室端面向外延伸0.2m,密封后内部容积约1m³。泄压口为正方形,边长分别为2、5、15和20mm。

试验样品为质量50g某温压炸药(TBE),主要成分为奥克托今(HMX)、铝粉和黏结剂,爆热约为TNT的1.8倍。样品均为长径比约1:1的压制柱形裸药,密度1.86g/cm³,以5g压装JH-14炸药为传爆药,用8号电雷管在药柱上端面中心起爆。

实验时,将药柱悬挂于方形爆炸室的中心位置,准静态压力测点位于侧壁面水平中心线上,共计2个,距该面中心点的水平距离分别为0.45m和0.60m。

准静态压力测试采用西安近代化学研究所自制的准静态压力测试组件,主要包括进气孔、管体、螺旋杆、铜垫片、传感器安装座、压力传感器,结构如图1所示,通过螺旋杆上的沟槽结构传递内爆炸压力,可滤掉冲击波高频分量,实现低频准静态压力的直接测量^[9]。压力传感器选用昆山双桥传感器测控公司的CYG400型压阻式压力传感器,其测量精度0.5级。经激波管校准,测试组件压力上升时间为0.24ms。

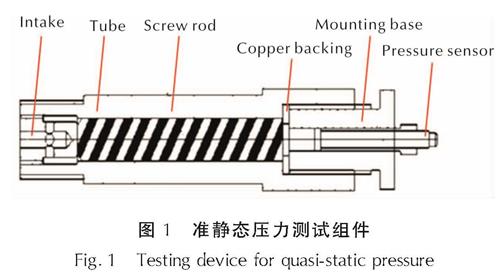
图1 准静态压力测试组件
Fig.1 Testing device for quasi-static pressure

• 2.1 不同泄压条件内爆炸的准静态压力变化

  开展了方形泄压口边长(a)分别为20、50、150和200mm条件下的内爆炸试验,并与密闭内爆炸试验进行对比,得到的准静态压力时程曲线如图2所示。需要说明的是,由于金属爆炸室是热的良导体,罐体内的高温会快速传递到空气介质中,导致罐体内温度降低,未设置泄压口时的准静态压力也缓慢下降。

  从图2可以看出,随着泄压口面积的增加,准静态压力峰值及峰值到达时间均减小。密闭时准静态压力峰值为0.312MPa,泄压口边长分别为20、50、150、200mm时的准静态压力峰值较密闭时分别下降了0.96%、4.81%、24.68%和37.50%。密闭时和泄压口边长为20、50mm时的峰值到达时间均约为40ms,泄压口边长为150、200mm时的峰值到达时间分别为35ms和32ms。

  

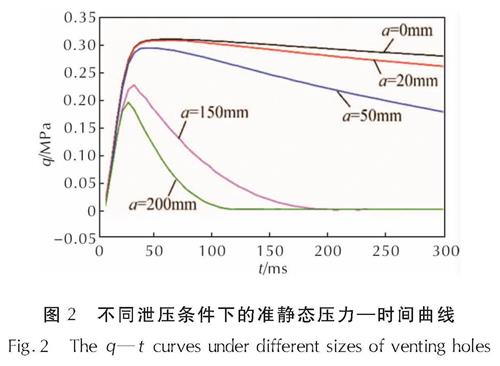
  图2 不同泄压条件下的准静态压力—时间曲线
  Fig.2 The q—t curves under different sizes of venting holes

  从图2还可看出,随着泄压口面积的增加,准静态压力达到峰值后的下降速率随之加快,压力恢复到大气压所需的时间减小。泄压口边长为150和200mm时准静态压力下降到大气压所需的时间分别为125ms和190ms,而截止350ms,密闭和泄压口边长分别为20、50mm时的准静态压力分别维持在0.274、0.252和0.156MPa,较峰值分别下降了12.2%、18.4%和47.5%。

• 2.2 泄压口面积对压力下降速率的影响

  准静态压力下降速率随时间变化曲线dq/dt—t如图3所示。

  

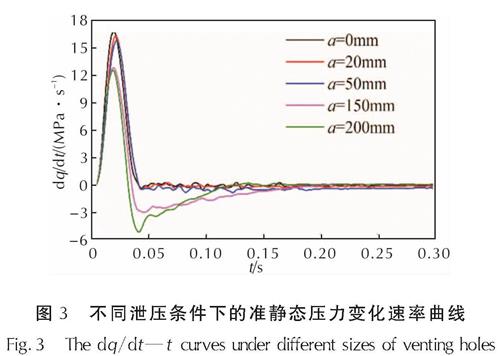
  图3 不同泄压条件下的准静态压力变化速率曲线
  Fig.3 The dq/dt—t curves under different sizes of venting holes

  从图3可以看出,dq/dt—t曲线先从0迅速上升至最大值然后再迅速下降到0,对应的准静态压力q上升时也可分为两个阶段:先急速增加后再相对缓慢地增加到压力峰值。准静态压力可分为两部分:一部分是温压炸药瞬时爆轰反应产生大量的气体和释放的大量热引起的有限空间的压力急速上升,表现为 dq /dt—t 曲线上升段,由温压炸药中的HMX含量决定; 另一部分是爆轰产物与爆炸室内空气、产物与产物之间发生后燃烧释放的热继而导致有限空间内气体压力相对缓慢地上升,表现为dq/dt—t曲线从峰值下降到 0 段,由金属燃料含量和空气中参与反应的氧气量决定。

  从图3还可以看出,dq/dt—t曲线下降到0后的变化趋势存在较大差异。当泄压口面积较小(对应图3中的a≤50mm)时,dq/dt值稍小于0且随时间t的增加变化不大,截至到0.3s时仍未回升到0,说明准静态压力曲线下降较为平缓; 当泄压口面积较大时,dq/dt—t曲线先迅速下降至最小值后再缓慢回升至0,对应的准静态压力下降时先急速下降后再缓慢下降逐渐恢复到大气压。这是由于压力泄放是从爆炸瞬间开始,只是在开始极短暂的时间内,相比于压力的迅速增加,压力泄放可以忽略。随着准静态压力上升减缓,压力泄放开始占据上峰,准静态压力上升停止后泄放速率迅速达到最大。随着约束空间的准静态压力不断降低,dq/dt逐渐回升。泄压口面积越大,dq/dt从最小值回升至0所需的时间越短。

• 2.3 准静态压力的工程计算模型

  假设爆炸气体产物为理想气体绝热模型,忽略爆炸容器的传热和固态产物所占体积。密闭条件下,内爆炸准静态压力峰值q₀与装药量m和内爆炸容积V密切相关^[11],有

  q₀=κ(m/V)^λ(1)

  式中:m为爆炸装药质量,kg; V为内爆炸容积,m³; κ、λ为炸药特征系数,根据其他工况下开展的试验结果,拟合得到样品的κ=1.796,λ=0.585。

  在有泄压口的约束体内的爆炸准静态压力峰值与泄压口面积A和内爆炸容积V密切相关,准静态压力峰值是比例泄压面积A/V^2/3的单值函数^[4-5],即

  (q_A)/(q₀)=f(A/(V^2/3))(2)

  式中:q_A为泄压口面积A时的内爆炸准静态压力峰值,MPa; q₀为密闭时的内爆炸准静态压力峰值,MPa; A为泄压口面积,m²; V为内爆炸容积,m³。以A/ V^2/3为横坐标、q_A/q₀为纵坐标作图,结果见图4。由图4可见,随着A/V^2/3的增加,q_A/q₀呈指数衰减。拟合得到:

  (q_A)/(q₀)=e^{-11.98A/(V2/3)}(3)

  Weibull^[1]认为,当A/V^2/3=0.0215时可以忽略排气口对准静态压力的影响。由式(3)可得到此时q_A/q₀=0.773,准静态压力峰值相对于密闭时下降了22.7%,对炸药内爆炸威力的影响已不能忽略。若峰值压力偏差不大于10%时可忽略排气口的影响,应满足A/V^2/3≤0.0085。

  

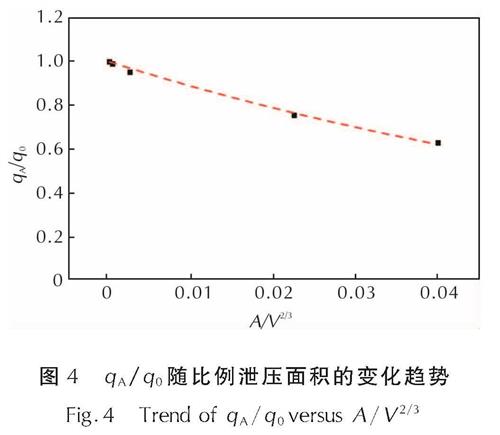
  图4 qA/q0随比例泄压面积的变化趋势
  Fig.4 Trend of qA/q0versus A/V2/3

  Proctor等^[2]、Kinney等^[3]研究得到了泄压结构中准静态压力随时间衰减的关系式:

  ln(q(t))/(p₀)=ln(q_A)/(p₀)-2.130τ^-(4)

  式中:p₀为大气压强; τ^-为无量纲时间,其计算式为:

  τ^-=(A/(V^2/3))((c₀t)/(V^1/3))(5)

  式中:c₀为空气声速; t为时间。将式(5)带入式(4),移项积分整理后,得到准静态压力的一般模型:

  q(t)=q_A?e^-ct(6)

  式中:c是与A/V相关的系数,可根据试验数据进行拟合,式(6)与Ethridge^[15]提出的冲击波压力—时间历程方程形式相同,但拟合精度相对较差,布罗德等^[16]给出了包含更多参数的修正公式。参考前人工作,给出式(6)的优化形式:

  q(t)=q_A?e^{α t+β t2}(7)

  式中:α、β是与A/V相关的系数。忽略准静态压力的上升时间,即峰值到达时刻t=0,式(7)中的指数多项式中常数项为0。按照式(7)对试验数据进行拟合,得到不同A/V条件下的α、β值,结果如表1所示。由表1可见,α、β值随着A/V的增加而减小。

  

  表1 不同A/V条件下的α、β值
  Table 1 Values of α and β under different A/V

  对α、β进行多项式拟合,得到α=-0.47-561.5(A/V)+4657.7(A/V)²,β=0.108-221038(A/V)²,式中的A、V均取国际单位时的量值,这样α、β值的量纲均为1。将式(3)、α和β代入式(6),得到泄压条件下的准静态压力为:

  q(t)=q₀e^{-11.98A/(V2/3)}?e^{[-0.47-561.5(A/V)+4657.7(A/V)2]}t+

  [0.108-221038(A/V)²]t²(8)

  将式(8)的计算结果与4种不同泄压口大小的试验结果进行对比,如图5所示。由图5可知,公式(8)计算结果与试验测得的准静态压力—时间曲线吻合较好,可用于不同泄压条件下的温压炸药内爆炸准静态压力预测。

  

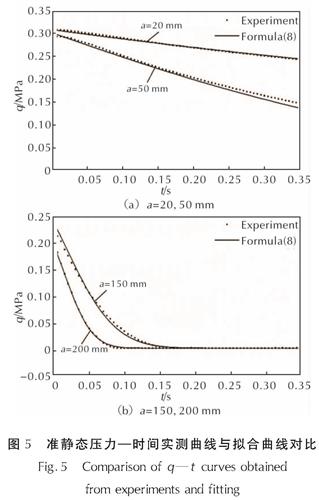
  图5 准静态压力—时间实测曲线与拟合曲线对比
  Fig.5 Comparison of q—t curves obtained from experiments and fitting

(1)泄压口面积对内爆炸准静态压力有着显著的影响。随着泄压口面积的增加,准静态压力峰值、峰值到达时间、最大上升速率和持续时间均减小,到达峰值后的下降速率增加。

(2)准静态压力峰值是泄压口面积与密闭空间容积的三分之二次方的比值A/V^2/3的单值函数。本实验得到有泄压口时的准静态压力峰值q_A与密闭时的准静态压力峰值q₀关系为(q_A)/(q₀)=e^-11.98A/(V^2/3)。当A/V^2/3≤0.0085时,峰值压力下降不大于10%,文献中当A/V^2/3≤0.0215时可忽略泄压口影响的结论有待商榷。

(3)泄压条件下,实时准静态压力q(t)与其峰值q_A的关系为q(t)=q_A?e^{αt+β t2},其中α、β是泄压口面积与密闭空间容积比值A/V的函数,α、β均随着A/V的增加而减小。