水下爆炸的气泡演变是一个复杂的过程,在水下武器的实际应用中,爆炸所产生的冲击波、气泡脉动以及水射流都承载着一定的毁伤效果^[1-5]。近代以来围绕水下爆炸开展了诸多理论^[6-7]与实验研究^[8-10],同时随着计算机技术的发展,数值模拟在水下爆炸领域有着重要作用^[11-14],帮助解决许多依靠实验难以观察与解决的问题,从而推动水下武器的发展。

许多水下武器因结构等的需求,采用柱形装药的方式,而柱形装药的长径比不同也会影响爆炸气泡的演化过程以及爆炸载荷。Zhang等^[15]通过LS-DYNA数值模拟水下爆炸气泡现象,并与实验对比,讨论不同长径比炸药在不同边界条件水下爆炸的气泡动力学行为差异。马腾等^[16]利用AUTODYN软件建立二维轴对称模型,开展长径比为1:2到10:1的柱形TNT炸药在无限水域的爆炸数值模拟,分析不同长径比对冲击波压力分布以及传播方向的影响,得到当长径比大于1:1时,炸药轴向冲击波压力衰减速率大于径向衰减速率,冲击波压力随着方向角增大而增大等结论。刘磊等^[17]利用AUTODYN软件分析长径比对远场压力峰值分布的影响,结果表明随着长径比的增大,装药形状对于冲击波的影响可以传递到更远的距离。对于柱形装药爆炸后形成的水射流,黄超等^[18]利用实验得出柱形装药TNT爆炸后产生的水射流存在形态差异,并通过实验现象观察出当药柱水平放置引爆时会产生不对称的水射流。针对板下气泡的动力学行为研究,Chen等^[19]通过高速摄像捕捉板下气泡演化图像,结合数值模拟分析了水下爆炸气泡对刚性壁面的压力作用及机理。目前对于使用数值模拟讨论长径比对板下气泡动力学行为影响的研究较少,且上述研究多从实验角度观测不同长径比柱形装药水下爆炸所产生的气泡行为与射流现象,难以得到射流的清晰图像以及数据。

本研究利用ABAQUS有限元软件建立三维模型,对不同长径比的炸药近场水下爆炸气泡动力学行为进行数值模拟,得到爆炸气泡演化图像、射流图像以及载荷信息。通过相应实验证明数值模拟的可行性。最后通过系列仿真研究炸药在不同的起爆状态下,长径比对爆炸气泡动力学行为的影响。结合数值模拟以及实验,系统讨论了不同长径比炸药在不同初始摆放条件以及起爆方式下的气泡动力学行为,从气泡以及射流图像反映长径比对于爆炸气泡的影响。

• 1.1 模型设置

  采用ABAQUS软件的CEL算法对固支方板下的水下爆炸进行数值模拟。使用欧拉域划分材料体积分数的方法进行建模。将水、空气以及炸药材料赋予欧拉网格,而板结构采用拉格朗日网格进行定义。总体模型圆柱形炸药竖直爆炸的工况采用1/4建模,水平装药因为考虑到起爆点选取问题所以采用1/2建模,物理建模如图1所示。

  

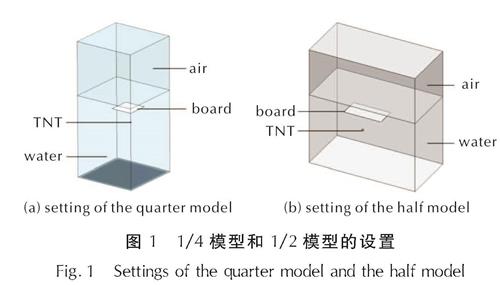
  图1 1/4模型和1/2模型的设置
  Fig.1 Settings of the quarter model and the half model

  模型总体欧拉域为1m×1m×2.2m的长方体,上方1m×1m×0.85m长方体为空气区域,水域为下方1m×1m×1.35m区域。爆距采取炸药中心到板底的距离。

  因整体欧拉区域较大所以划分网格采用局部加密以及渐变网格划分方法,最密的网格部分集中在炸药中心位置,确保炸药当量的准确性以及压力数据的准确,如图2所示。其中加密区域网格为3mm,过渡区域网格由3mm逐渐增至40mm。欧拉域的网格类型为EC3D8R,板的网格类型为S4R。其中1/4模型网格总数约为250万,1/2模型网格总数约为502万。

  

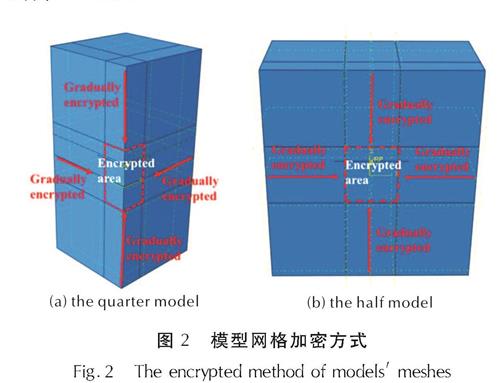
  图2 模型网格加密方式
  Fig.2 The encrypted method of models' meshes

  模型的各项边界条件设定为,对称面设置为对称边界条件。模型顶部压力设为一个标准大气压,底部设置为标准大气压加上相应水深的压力。模型侧面水的区域压力设置为标准大气压加上梯度水压。并对侧面区域统一设置为无反射边界。板的中心参考点设置为固定,因为板面的刚性特性,所以板保持固定状态。针对模型整体区域设置环境温度15℃,以及重力常数9.8N/kg。设置炸药的起爆点为原点,以移动整体模型来模拟不同起爆点爆炸后的气泡动力学行为特征。数值模拟采用通用接触算法,物质之间切向无摩擦力,法向接触方式为硬接触。

• 1.2 材料参数

  ABAQUS软件的CEL算法经常用于求解流固耦合问题。拉格朗日网格用于描述模拟固体结构的形变,欧拉网格满足材料在单元之间的流动,所以对于求解水下爆炸流固耦合问题有着重要的应用价值。

  • 1.2.1 爆炸产物方程

    ABAQUS对于水下爆炸爆轰产物利用JWL状态方程进行描述^[20]。JWL状态方程为压力关于密度以及热力学能的函数,其具体形式如下:

    

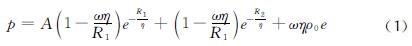
    式中:p为爆炸产物压力; η为相对密度,η=ρ/ρ₀; ρ为水的密度; ρ₀为TNT理论密度; e为TNT比内能; A、B、ω、R₁、R₂为常数。在模型建立中设置A=373.77GPa,B=3.7471GPa,R₁=4.15,R₂=0.9,ω=0.35,e=3.8×10⁶J/kg,ρ₀=1630kg/m³。

  • 1.2.2 理想气体方程

    对于爆炸环境中的空气利用理想气体方程进行定义,理想气体方程形式为:

    p+p_A=ρ R(θ-θ_Z)(2)

    式中:p_A为环境压力; ρ为空气密度; R为气体常数; θ为环境温度,θ_Z为绝对零度所对应的温度。此外还要设置空气的比热c。相关参数见表1。

    表1 理想气体方程参数
    Table 1 Parameters of the ideal gas equation

    

  • 1.2.3 水的状态方程

    水域部分材料使用ABAQUS软件提供的U_s—U_p状态方程进行设置。U_s—U_p状态方程假设流体不可压缩且密度较小。参考Mie-Grüneisen状态方程形式为:

    p-p_H=Γρ(E_m-E_H)(3)

    式中:p为压缩材料压力; p_H为Hugoniot压力; E_m为比热力学能; E_H为Hugoniot内能; Г为Mie-Grüneisen系数,满足Гρ=Г₀ρ₀,Г₀为绝对零度时的Mie-Grüneisen系数,ρ₀为参考密度。

    由Hugoniot关系,可得E_H与p_H之间的关系为:

    

    其中η=1-ρ₀/ρ。

    Hugoniot压力p_H为:

    

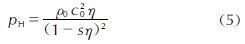
    根据U_s—U_p状态方程,冲击波速度U_s和粒子速度U_p的关系式可以表示为:

    U_s=c₀+su_P(6)

    同时根据ρ(U_s-U_p)=ρ₀U_s,可将Mie-Grüneisen方程写为:

    

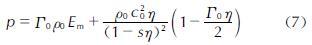
    式中:c₀为声速; ρ₀为水的密度; s为材料相关系数; Г₀为Mie-Grüneisen系数。各项参数设置见表2。

    表2 Mie-Grüneisen方程参数
    Table 2 Parameters of the Mie-Grüneisen equation

    

• 2 数值模型的验证

  • 2.1 实验设置

    为验证数值模拟的准确性,开展固支方板下不同长径比炸药的水下爆炸实验。实验在江苏永丰机械有限公司的2m×2m×2m的水箱中展开。图3为实验示意图,固支方板爆炸实验将炸药固定在板下相应爆距引爆。爆炸中心水平位置相应距离悬有水下传感器,在炸药中心正上方板的位置固定有壁压传感器来记载冲击波及气泡脉动所引起的压力信号。利用Phantom高速摄像机记录气泡演变图像。

    

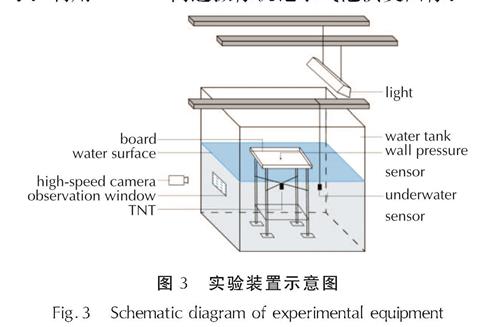
    图3 实验装置示意图
    Fig.3 Schematic diagram of experimental equipment

    为了研究不同长径比炸药近场水下爆炸的气泡演化规律以及载荷特性,开展了长径比为1:1和2:1的2.5g柱形TNT在板底起爆的水下爆炸实验。炸药采用竖直放置的方法,起爆点为炸药底部。

    实验所采用的固支方板尺寸为70cm×70cm,厚度为1cm,焊接在底部钢架上,底部钢架全部采用实心钢材,支架由4根直径2cm实心钢柱以及4块20cm×20cm×0.5cm底板组成,尽可能使结构在爆炸过程中不会产生明显形变以及剧烈晃动,更加贴近数值模拟模型对于固支方板设定的刚性条件。

  • 2.2 实验与模拟结果对比

    图4是长径比为1:1与2:1的炸药板下爆炸实验与数值模拟的气泡演化图像对比。实验图像为Phantom高速摄影机记录影像,数值模拟结果采用爆炸产物边界显示。由图4可知,长径比为1:1的炸药实验图像在约20.31ms时气泡膨胀到最大半径,数值模拟气泡在约20.18ms时膨胀到最大半径,相差0.13ms; 长径比为2:1的炸药水下爆炸实验图像显示气泡在约21.88ms膨胀到最大半径,数值模拟结果为约20.82ms时气泡膨胀到最大半径,相差1.06ms。实验与数值模拟的气泡均反映出气泡在爆炸之后的膨胀过程,以及膨胀到一定尺寸后受到Bjerknes力影响而产生的气泡被板面吸引的现象。实验与数值模拟的气泡在动力学行为上保持着高度的一致性。两种长径比的炸药爆炸产生的气泡膨胀与收缩现象、周期数值模拟结果都与实验吻合。将实验与数值模拟的气泡演化图像进行对比可得,关于气泡演化图像,数值模拟具有较好的准确性。

    图5为实验与数值模拟气泡半径随时间变化的对比图。

    

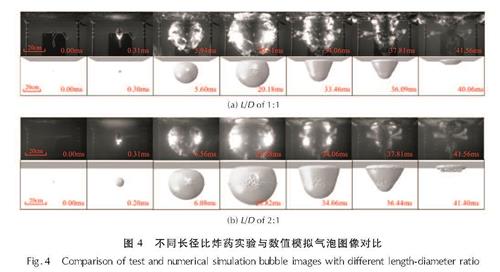
    图4 不同长径比炸药实验与数值模拟气泡图像对比
    Fig.4 Comparison of test and numerical simulation bubble images with different length-diameter ratio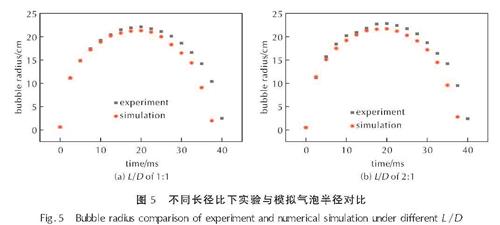

    

    图5 不同长径比下实验与模拟气泡半径对比
    Fig.5 Bubble radius comparison of experiment and numerical simulation under different L/D

    由图5(a)可得长径比为1:1的炸药在板下爆炸后,实验气泡最大半径为22.1cm,模拟所得气泡最大半径为21.3cm,相差0.8cm,误差约3.62%; 实验气泡膨胀到最大半径用时约20.31ms,模拟气泡膨胀到最大半径用时约20.18ms,相差0.13ms。由图5(b)长径比为2:1的炸药在板下爆炸后,实验测得气泡最大半径约为22.8cm,模拟结果气泡最大半径为21.7cm,相差1.1cm; 实验气泡膨胀到最大半径用时约21.88ms,模拟气泡膨胀到最大半径用时约20.82ms,相差1.06ms。即数值模拟可以较好地模拟出气泡的真实半径与周期。

    图6是15cm爆距、长径比为1:1的炸药在水下爆炸实验与模拟的板下压力时程曲线对比。其中实验测得冲击波压力峰值为81.21MPa,数值模拟测得冲击波压力峰值为75.57MPa,相差5.64MPa,误差约为6.94%。实验测得板下气泡脉动水射流阶段所受压力峰值为20.46MPa,数值模拟测得结果约为22.67MPa,相差2.61MPa。实验所得曲线气泡脉动水射流阶段峰值产生时间为40.07ms,数值模拟测得气泡脉动水射流阶段峰值产生时间为38.45ms,相差约1.62ms。数值模拟结果与实验基本一致,说明了数值模拟的准确性。

    

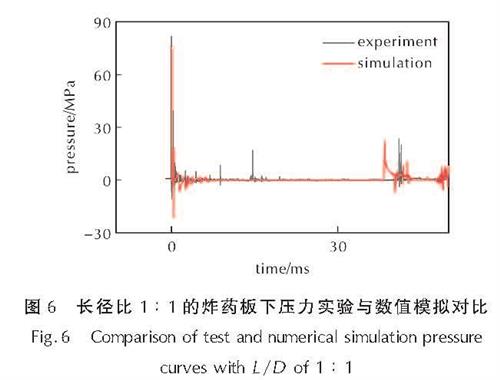
    图6 长径比1:1的炸药板下压力实验与数值模拟对比
    Fig.6 Comparison of test and numerical simulation pressure curves with L/D of 1:1

    结构在爆炸后先受到冲击波的冲击,即压力时程曲线图第一个峰值,随后结构受到气泡膨胀作用的影响,如图4(a)实验图像0ms到20.31ms,随后因气泡内部压力小于外部压力,所以气泡开始收缩,对结构产生吸力,在收缩到一定程度后,在气泡底部形成竖直向上的水射流,对结构造成冲击,同时伴随气泡脉动的影响,在压力时程曲线上产生第二次波峰,如图6中40ms左右传感器记录的压力数据。

  • 2.3 网格敏感性验证

    图7是不同尺寸网格下长径比1:1的炸药距板下15cm起爆后在板下压力单元数值模拟结果。当加密区域网格为6mm时,模拟结果误差太大不具有参考价值。当加密区域网格尺寸为3mm时,冲击波峰值为75.57MPa; 当进一步细化加密网格到2mm后,数值模拟结果得到冲击波峰值为68.31MPa,相差约7.26MPa,3mm网格数值模拟结果更接近实验值,进一步加密网格不会对数值模拟结果与实验拟合显著提升。结合图4,3mm网格模型计算的气泡在形态演化上具有较好的收敛性。加密网格到2mm后网格数量将是原网格数的3倍,计算周期较大延长,由原先的单个算例48h的计算周期延长到单个算例需要120h以上,所以加密区域网格尺寸选择为3mm。

    

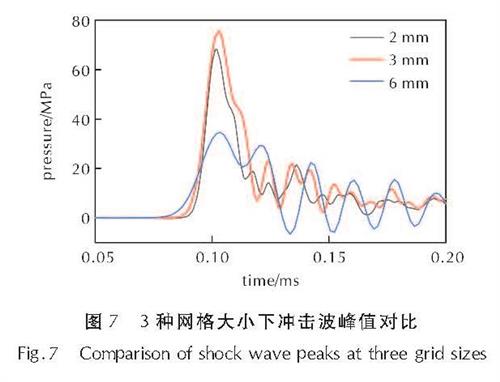
    图7 3种网格大小下冲击波峰值对比
    Fig.7 Comparison of shock wave peaks at three grid sizes

• 3 炸药竖直摆放爆炸气泡演化过程模拟

  根据模拟工况建立方法,对不同长径比炸药竖直起爆展开系列模拟。当炸药长径比不同时,爆炸产生的气泡初始形态也不相同。由于固支方板对于气泡有Bjerknes效应的影响,气泡初始形态有可能会与Bjerknes效应对气泡共同影响,从而使得气泡产生不同的动力学行为,所以对于不同长径比的炸药水下爆炸动力学行为研究要分为竖直装药与水平装药进行讨论。

  • 3.1 起爆点相同

    当炸药初始摆放方式为竖直摆放时,主要有3种不同的起爆方式,分别为:底部起爆、中间起爆和顶端起爆。实验所采用的起爆方式为底部起爆,所以针对长径比为5:1、10:1、20:1的3种柱形炸药首先都采取底部起爆的方式进行数值模拟。

    图8是长径比为5:1、10:1和20:1的炸药在板下15cm起爆点同为底部时的爆炸图像。当炸药为竖直装药时,3种长径比的炸药起爆点同为底部起爆时,爆炸后形成的气泡在0.20ms时有显著的形状区别,随着气泡的演化这种区别会越来越小,在6.32ms时气泡形状差别已经很小,随后气泡膨胀为近乎相同的形状。气泡在受到板的Bjerknes力与浮力的影响而产生显著形变之前就已经膨胀至相同形状,所以长径比对于气泡后期的演化造成的影响较小。即当长径比为20:1以下的炸药为竖直装药时,长径比对于爆炸气泡形态的影响主要集中在炸药膨胀初期短时间内的形态上,经过膨胀气泡迅速成为同样的形态,并不对后续气泡演化造成明显影响。

    

    图8 不同长径比炸药在板下15cm爆炸气泡图像
    Fig.8 Bubble images of different L/D explosives exploding 15cm below the plate

    图9是爆距为15cm时,长径比5:1、10:1与20:1的炸药底部起爆板下爆炸的射流图像,以速度为变量绘制气泡内部速度云图。射流速度云图的速度单位均为m/s。由图9可知当炸药初始摆放方式为竖直放置时,3种长径比的炸药在相同起爆方式下,爆炸气泡产生的射流在形成时间、形态上无明显区别。

    

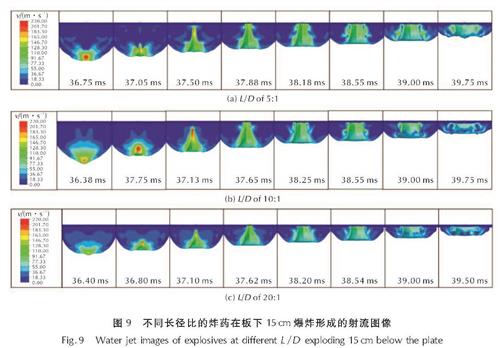
    图9 不同长径比的炸药在板下15cm爆炸形成的射流图像
    Fig.9 Water jet images of explosives at different L/D exploding 15cm below the plate

    图10是射流顶端速度随时间的变化曲线。由图10可得3种长径比炸药爆炸后形成的射流最大速度相似,长径比为5:1的炸药爆炸产生的水射流在达到最大速度后更快地衰减,衰减后射流速度略低于另外两种长径比炸药爆炸产生的射流速度。

    

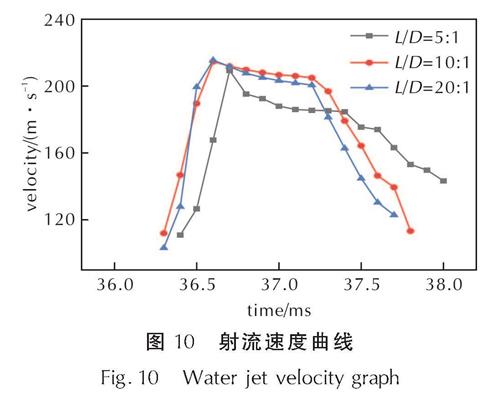
    图10 射流速度曲线
    Fig.10 Water jet velocity graph

    当炸药竖直摆放时,爆炸形成的射流呈现出底部较粗顶部较细的特征,在高度一定的情况下,射流平均宽度取与射流截面积相等的等高长方形边长d,见图11。

    

    图11 射流平均宽度示意图
    Fig.11 Schematic diagram of the average width of the water jet

    图12是竖直摆放的不同长径比炸药爆炸后形成射流的平均宽度随时间变化的曲线,可以看出3种长径比炸药爆炸后所形成的射流不论是平均宽度还是射流宽度增长速度都相近,结合射流速度云图可得3种长径比炸药竖直摆放爆炸后形成的射流形态与演化过程相似。

    

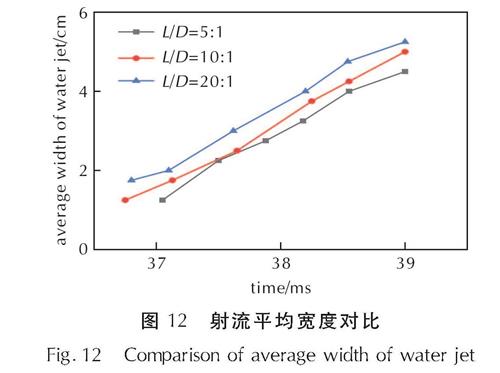
    图12 射流平均宽度对比
    Fig.12 Comparison of average width of water jet

  • 3.2 起爆点不同

    图13分别为长径比20:1的炸药底部起爆、中间起爆、顶端起爆3种不同起爆方式下的气泡图像。同一长径比的炸药在3种起爆方式下产生的气泡都在爆炸初期呈现一定的竖长特性,随着演化过程逐渐统一为椭圆形,气泡都在18ms左右膨胀到最大半径,所以气泡的演化过程、形态以及周期上都无明显差别。图14是长径比为20:1的炸药3种不同起爆方式下的射流图像。3种气泡射流形成时间都在37ms左右,且射流形态相似。得出炸药初始摆放方式为竖直摆放且长径比固定时,起爆位置对气泡动力学行为不产生显著影响。

    

    图13 长径比20:1的炸药不同起爆位置爆炸气泡图像
    Fig.13 Bubble images of explosives with a L/D of 20:1 at different detonation positions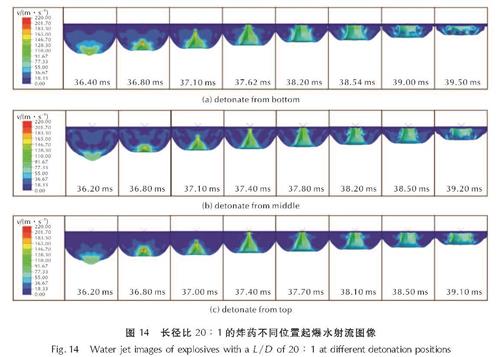

    

    图14 长径比20:1的炸药不同位置起爆水射流图像
    Fig.14 Water jet images of explosives with a L/D of 20:1 at different detonation positions

    图15是不同起爆点引爆炸药所产生的射流速度时程曲线。由图15可以看出,3种起爆点射流形成的时间接近。起爆点位于炸药上端中心点时射流速度最大,最大速度可达到233.7m/s; 其次是起爆点位于炸药下端中心点,最大速度为215.5m/s; 当起爆点位于炸药中心时射流速度最小,最大速度为181.4m/s。即起爆点虽然对射流形态无明显影响,但会影响射流速度。

    

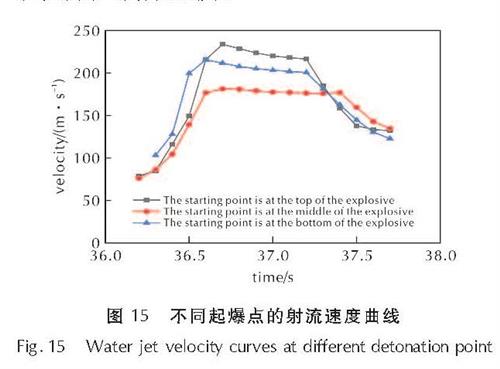
    图15 不同起爆点的射流速度曲线
    Fig.15 Water jet velocity curves at different detonation point

• 4 炸药水平摆放爆炸气泡演化过程模拟

  • 4.1 起爆点为炸药端部中心

    图16为长径比20:1的炸药水平装药且起爆点为炸药端部的中心位置时,爆距15、20、25cm下的气泡演化图像。由于起爆位置处于炸药一侧,所以气泡在膨胀过程中形态保持着一定的不对称。当气泡膨胀到一定尺寸后,因受到板面Bjerknes效应的影响,气泡受到板的作用被拉长,同时进行气泡的收缩过程。

    图17为爆距25cm时,长径比为5:1、10:1、20:1的3种炸药爆炸气泡水射流阶段的演化图像。图像为以速度为变量绘制的气泡内部速度云图。由图17可以看出,当长径比在5:1到20:1的范围内,炸药长径比对于气泡的水射流形成时间无明显影响。但随着长径比的增加,水射流在气泡内部的宽度也会随之增加,长径比为5:1的炸药爆炸后当气泡塌缩形成水射流时,射流在气泡内部相对处于竖直向上的状态,对目标造成更集中的冲击; 而当长径比增大时,水射流直径在气泡内部不断扩大,当炸药长径比为20:1时,水射流不对目标造成明显冲击。3种长径比炸药射流形成时间都在36.50ms左右,所以炸药长径比对于射流形成时间并不造成显著影响,同时3种射流在同一时间的速度也相近,但是因为炸药长径比的影响,长径比过大的炸药爆炸后产生的射流会因直径扩大迅速而导致较早溃散。

    图18为射流顶部宽度随着时间变化的示意图,依照Liu等^[21]对于射流宽度的定义,由于射流形态的不规则性,可以在截面面积相同的情况下,射流平均宽度等效为与射流截面积相同的l×d矩形的边长d,如图19,即射流平均宽度为:

    

    

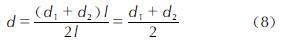
    图16 长径比20:1的炸药在板下不同距离的爆炸气泡图像
    Fig.16 Bubble images of explosives with a L/D of 20:1 at different distances under the board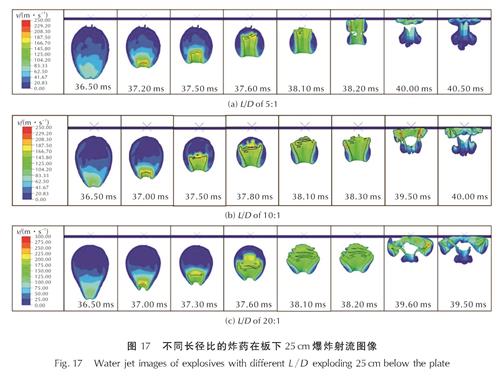

    

    图17 不同长径比的炸药在板下25cm爆炸射流图像
    Fig.17 Water jet images of explosives with different L/D exploding 25cm below the plate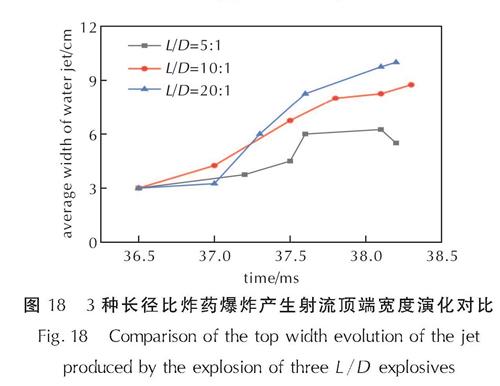

    

    图18 3种长径比炸药爆炸产生射流顶端宽度演化对比
    Fig.18 Comparison of the top width evolution of the jet produced by the explosion of three L/D explosives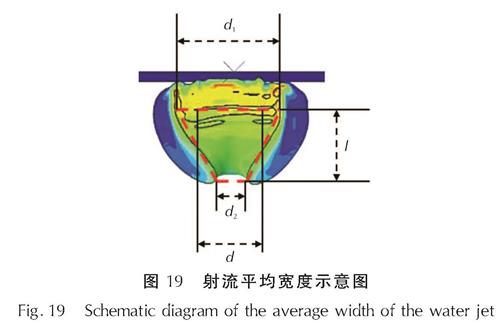

    

    图19 射流平均宽度示意图
    Fig.19 Schematic diagram of the average width of the water jet

    由图19可以清晰看出,长径比越大的炸药爆炸后产生的射流在气泡内部宽度增加越快。随着射流在气泡内部的演化射流的平均宽度也更大。

    图20是图17的3种工况模拟结果板下测得的射流阶段压力曲线,取板中心下一格网格输出压力时程曲线,见图21。由图20可得当长径比为5:1到20:1的范围内,随着长径比的减少,水射流阶段所造成的压力在总体上会越大,印证了关于射流图像得出的较小长径比的炸药会对目标产生更加集中的射流的结论。可知长径比的大小会影响射流对目标造成的压力,影响射流的打击效果。

    

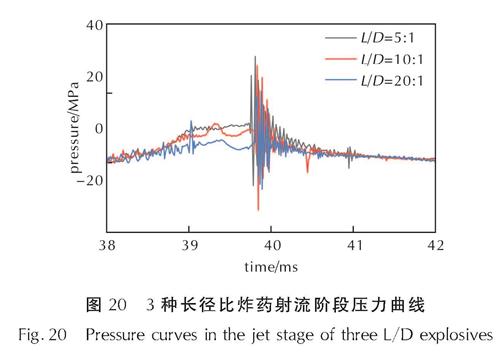
    图20 3种长径比炸药射流阶段压力曲线
    Fig.20 Pressure curves in the jet stage of three L/D explosives

    

    图21 网格选取位置示意图
    Fig.21 Schematic diagram of grid selection location

    图22是当炸药长径比为20:1时,在爆距15、20、25cm下气泡射流的形成过程图像。

    

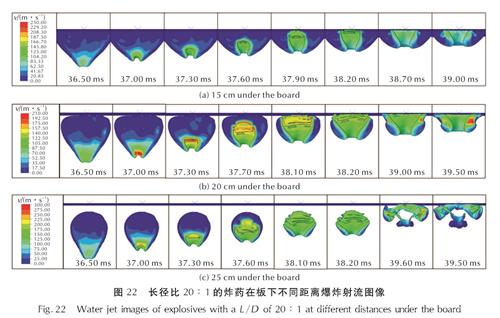
    图22 长径比20:1的炸药在板下不同距离爆炸射流图像
    Fig.22 Water jet images of explosives with a L/D of 20:1 at different distances under the board

    由图22可得长径比20:1的炸药爆炸产生的射流在气泡内部呈现不断变粗的趋势。但当爆距较小(如15cm)时,因气泡被板面吸引,气泡更贴近板面,所以水射流更容易击中目标板面。当爆距与炸药长径都比较大时,会出现射流在击打到目标之前就发生溃散的情形。

  • 4.2 起爆点为炸药中心

    图23是长径比为20:1的炸药在15cm板下,起爆点为炸药一侧和起爆点在炸药中心的爆炸气泡图像对比。由图23可以看出,不同的起爆位置对于爆炸气泡的演化无明显影响,当起爆点为炸药一侧时爆炸气泡在膨胀阶段呈现略微的不对称,起爆点为中心时爆炸气泡在膨胀阶段更加对称,但起爆位置不影响气泡的后续动力学行为。

    图24是爆距为15cm,长径比20:1的炸药水平引爆产生的气泡的射流图像。当引爆位置为炸药一侧时,射流会出现略微的倾斜,而当引爆点为炸药中间时,射流不发生倾斜。此外,引爆位置对于射流的形成时间、形状以及射流速度等无明显影响。当起爆点为炸药中心时,爆炸后形成的射流在气泡内部呈现相似的特性,射流顶端都会呈现不断变宽的趋势。

    

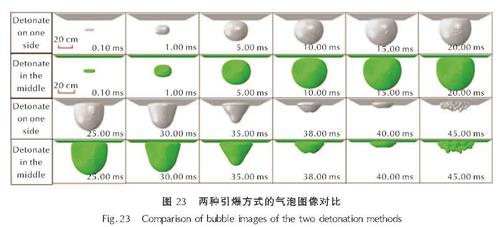
    图23 两种引爆方式的气泡图像对比
    Fig.23 Comparison of bubble images of the two detonation methods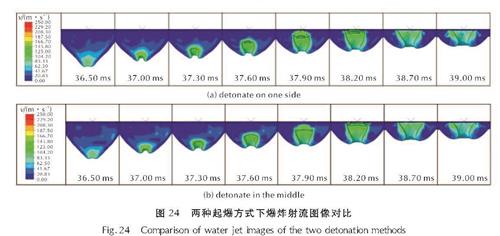

    

    图24 两种起爆方式下爆炸射流图像对比
    Fig.24 Comparison of water jet images of the two detonation methods

    图25是爆距为25cm,长径比20:1的炸药爆炸射流阶段对目标底部造成的压力时程曲线,压力曲线取自板中心下一格网格。由图25可得,起爆位置虽然会少许影响射流的形态,但并不影响射流对目标造成的载荷大小。

    图26是水平摆放炸药不同起爆位置射流平均宽度随时间的变化曲线,两种起爆位置形成的射流除了在形态上略有不同,射流平均宽度与宽度增加速度都近似。

    

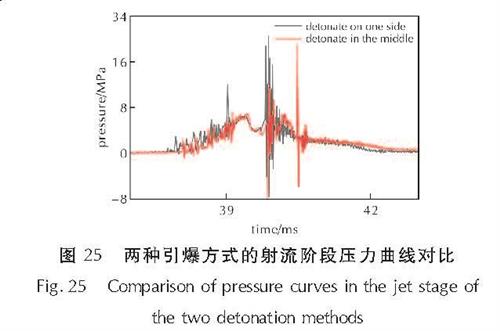
    图25 两种引爆方式的射流阶段压力曲线对比
    Fig.25 Comparison of pressure curves in the jet stage of the two detonation methods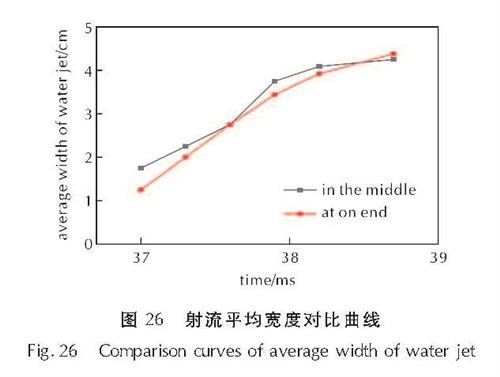

    

    图26 射流平均宽度对比曲线
    Fig.26 Comparison curves of average width of water jet

• 5 结 论

  (1)不同长径比的炸药不论在竖直装药还是水平装药条件下,长径比对于气泡演化动力学行为无明显影响。当炸药水平装药时,起爆点在一端或中心会造成气泡在演化过程中呈现轻微的不对称,但不影响总体气泡演化进程。

  (2)竖直装药时,不同长径比炸药对射流形态基本无影响; 水平装药时,长径比越大的炸药射流在气泡内部呈现宽度越大的趋势,从而影响射流载荷,总体趋势为射流越宽对壁面造成的载荷越小,。

  (3)竖直装药时,数值模拟的3种长径比的炸药爆炸后射流最大速度集中在210～220m/s,但长径比为5:1的炸药射流速度要明显低于另外两种炸药。不同起爆位置对于射流速度的影响规律总体为:顶端起爆形成的射流速度最大,达到233.7m/s,中心起爆的射流速度最小,仅181.4m/s,相差约25.05%。

• 参考文献

  • [1] 贾则,陈高杰,高浩鹏,等. 水下爆炸冲击波和气泡脉动载荷联合作用下舰船冲击响应研究 [J]. 中国测试,2018,44(12):28-32.
    
  JIA Ze, CHEN Gao-jie, GAO Hao-peng, et al. The Research of impact response of warship based on underwater explosion shock wave and bubble impulse [J]. China Measurement & Testing Technology, 2018, 44(12): 28-32.
  • [2]姚熊亮,刘文韬,张阿漫,等. 水下爆炸气泡及其对结构毁伤研究综述 [J]. 中国舰船研究,2016,11(1):36-45.
    
  YAO Xiong-liang, LIU Wen-tao, ZHANG A-man, et al. Review of the research on underwater explosion bubbles and the corresponding structural damage [J]. Chinese Journal of Ship Research, 2016, 11(1): 36-45.
  • [3]崔杰,李世铭,黄超,等. 射流冲击模型在水下爆炸实验中的应用研究 [J]. 高压物理学报, 2012,26(5):523-530.
    
  CUI Jie, LI Shi-ming, HUANG Chao, et al. Application reach of jet impact model in an underwater explosion experiment [J]. Chinese Journal of High Pressure Physics, 2012, 26(5): 523-530.
  • [4]ZHANG Yi-fan, et al. Study on the impact characteristics of underwater explosion bubble jets induced by plate structure[J]. Ocean Engineering, 2022,266: 11264.1-11264.19.
    
  • [5]伍俊,杨益,庄铁栓.水中爆炸作用机理及毁伤效应研究综述[J].火炸药学报,2016,39(1):1-13.
    
  WU Jun, YANG Yi, ZHUANG Tie-shuan. A review of research on action mechanism and damage effect of underwater explosion[J]. Chinese Journal of Explosives & Propellants(Huozhayao Xuebao), 2016,39(1):1-13.
  • [6]COLE R H. Underwater Explosion[M]. New Jersey: Princeton University Press, 1948: 118-127.
    
  • [7]ZAMYSHLYAEV B V, YAKOVLEV Y S. Dynamic Loads in Underwater Explosion, AD-757183[R]. Springfield:NTIS, 1972: 86-120.
    
  • [8]郑监. 浅水中爆炸水射流的形成机理研究[D].长沙:国防科学技术大学,2016.
    
  ZHENG Jian. The Research on the Forming Mechanism of Liquid Jet in Shallow Water Explosions[D].Changsha: National University of Defense Technology, 2016.
  • [9]MENON Suresh, LAL Mihir. On the dynamics and instability of bubbles formed during underwater explosions[J]. Experimental Thermal and Fluid Science, 1998, 16(4): 305-321.
    
  • [10]CHEN Si, QIN Jian, DENG Shuo, et al. Experimental and numerical studies on fixed steel sheets subjected to underwater explosion[J]. Materials, 2022, 15(18): 6419-6419.
    
  • [11]MA Wen-tao, ZHANG Xun-ning, Gilbert Christine, et al. Numerical simulation data of bubble-structure interactions in near-field underwater explosion[J]. Data in Brief, 2022, 43: 108337.
    
  • [12]秦业志,王莹,王志凯,等.小当量柱型装药水下近场爆炸固支单层方形钢板毁伤特性研究[J].振动与冲击,2021,40(7):29-36.
    
  QIN Ye-zhi, WANG Ying, WANG Zhi-kai, et al. Damage characteristics of fixed single-layer square steel plate under near-field underwater explosion of small equivalent column charge[J]. Journal of Vibration and Shock, 2021, 40(7): 29-36.
  • [13]李元龙,王金相,申向军,等. 水下爆炸冲击波作用下屏蔽装药的冲击引爆理论和仿真研究[J].振动与冲击,2019,38(11):31-36.
    
  LI Yuan-long, WANG Jin-xiang, SHEN Xiang-jun, et al. Initiation theory of shield explosive impacted by underwater explosion shock wave and its simulation[J]. Journal of Vibration and Shock, 2019, 38(11): 31-36.
  • [14]姚成宝,付梅艳,闫凯,等.基于Riemann问题的可压缩多介质流体数值模拟及在二维爆炸冲击波传播问题中的应用[J].火炸药学报,2020,43(3):254-261.
    
  YAO Cheng-bao, FU Mei-yan, Yan Kai, et al. Numerical simulation of multi-material compressible flows based on riemann problem and its application in two-dimensional blast wave propagation[J]. Chinese Journal of Explosives & Propellants(Huozhayao Xuebao),2020,43(3):254-261.
  • [15]ZHANG A-man, WANG Shi-ping, HUANG Chao, et al. Influences of initial and boundary conditions on underwater explosion bubble dynamics[J]. European Journal of Mechanics/B Fluids, 2013, 42: 69-91.
    
  • [16]马腾,王金相,刘亮涛,等.不同长径比柱形装药水下爆炸冲击波演化规律[J].振动与冲击,2022,41(8):149-157.
    
  MA Teng, WANG Jin-xiang, LIU Liang-tao, et al. Shock wave evolution of cylindrical charge with different slender ratios [J]. Journal of Vibration and Shock, 2022, 41(8): 149-157.
  • [17]刘磊,郭锐,裴善报,等.柱形装药水下爆炸远场冲击波压力峰值分布[J].振动与冲击, 2016,35(17):66-70.
    
  LIU Lei, GUO Yue, PEI Shan-bao, et al. Far-field shock wave peak pressure distribution for underwater explosion of cylindrical charges [J]. Journal of Vibration and Shock, 2016, 35(17): 66-70.
  • [18]黄超,汪斌,张远平,等.柱形装药自由场水中爆炸气泡的射流特性[J].爆炸与冲击,2011,31(3):263-267.
    
  HUANG Chao, WANG Bin, ZHANG Yuan-ping, et al. Behaviors of bubble jets induced by underwater explosion of cylindrical charges under free-field conditions [J]. Explosion and Shock Waves, 2011, 31(3): 263-267.
  • [19]CHEN Ying-yu, YAO Xiong-liang, CUI Xiong-wei. A numerical and experimental study of wall pressure caused by an underwater explosion bubble[J]. Mathematical Problems in Engineering, 2018, 2018(10):1-10.
    
  • [20]GAN N, LIU L T, YAO X L, et al. Experimental and numerical investigation on the dynamic response of a simplified open floating slender structure subjected to underwater explosion bubble[J]. Ocean Engineering, 2021, 219:108308.
    
  • [21]LIU L T, YAO X L, ZHANG A M, et al. Research on the estimate formulas for underwater explosion bubble jet parameters [J]. Ocean Engineering, 2018, 164:563-576.